Physics 2024, 20: Gauge Fixing in Functional Integration

An element of the S-matrix is determined by a functional integral with a Yang-Mills action functional S[A]

The integration measure is taken over a system of an uncountable number of degrees of freedom in 4-D spacetime, with an asymptotic gauge field configuration. The gauge copies need to be identified and factored out of the product before applying the integral. In a Lorentz-covariant regime, only specific points in the gauge orbit are allowed:

with an arbitrary su(N)-valued, gauge-invariant Lorentz scalar function K(x), group elements in adjoint representation R[ω] and ω-dependent shifts f[ω]. The measure is gauge-invariant, so the YM-action in the integrand is as well. This allows exchange of mutually invariant variables without introduction of additional factors, which also extends to the definition of the covariant derivative. The functional determinant of the operator can be written as a Gaussian functional integration over complex Grassmann scalar-fields.

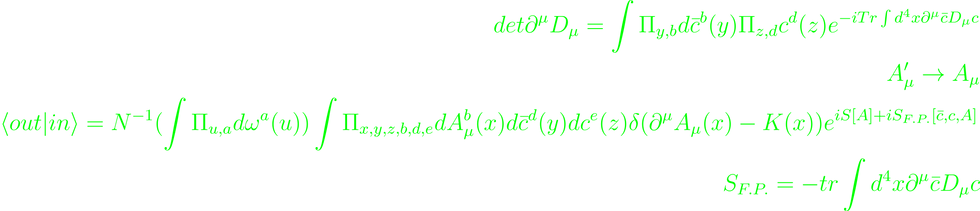
The kinetic component of the (fermionic) Grassmann-field c carries the wrong sign in the action, which implies so-called "ghost fields". Each ghost loop then requires an additional factor of -1. The gauge transformations are only integrated over as some factor, that can be ignored in qualitative reading of the functional integral. The functional integral has no dependence on K(x), and so its computation can be included as a factor with dependency of a "weight functional" F[K], which can be chosen almost freely.

The modified action sees contributions to cutting rules completely being based on unphysical phenomena canceled. This whole procedure is in reference to the Faddeev-Popov procedure. It doesn't fix the gauge completely, and arises from partial gauge invariance.