Physics 2024, 19: Spontaneous Gauge-Symmetry Breaking

A smooth curve in 4D spacetime has a "Wilson Line" along itself, defined through an exponential.

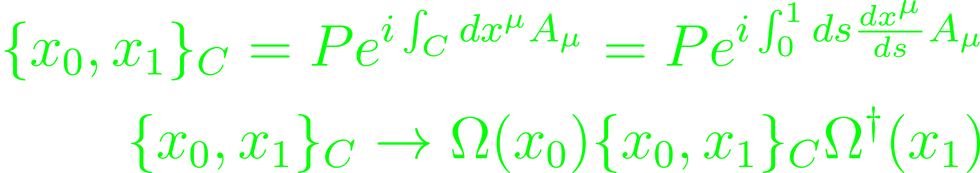
with a path-ordering operator P. It's an element of SU(N). If C is a closed loop, then {x, x} of the gauge field A locally transforms under adjoint representation. This results in a "Wilson loop". Shifting the base-point of the curve shifts the group element that determines the gauge transformation Ω.

is gauge invariant. The average of these quantities grows with the area of the contour of the curve.

Spontaneously gauge symmetry breaking can be introduced by non-invariance of the ground state under gauge transformation. Assume the existence of a scalar field ϕ and an extended ground state estimate. This means that the theory is equipped with a gauge-invariant potential V(ϕ), or an appropriate boundary condition. The scalar field ϕ transforms under an appropriate representation of SU(N). If ϕ is charged under the adjoint representation, the minimally extended Yang-Mills action is

The field modulus |ϕ| has a constant ground state expectation, and so the field can be decomposed to said constant expectation value with a perturbation. It can solve the classical Euler-Lagrange equations of motion, following from the Yang-Mills action. The resulting energy density is constant, thus proving the assumption valid, though the constant field-term may break gauge symmetry. Generally, its direction in su(N) can be chosen to be parallel to some generator. Neglecting the perturbation leads to the following Lagrangian

Commuting generators hint toward modes of A, which propagate as massless gauge-field excitations with 2 polarization states. There are exactly as many of these modes as SU(N) has ranks, which is N - 1. Symmetry-breaking generators get a mass, propagating with three polarization states.

These configurations can be developed toward finite actions, static energy, possibly per spatial line element. The first case is fairly natural in 4D Euclidean spacetime. The other two cases require non-trivial dependece of ϕ₀ on the spacetime. A Lie group that can be broken down to a subgroup H by a non-vanishing groun-state estimate, ϕ₀: G → H. ϕ₀ is invariant under gauge transformations emerging from H, so G/H consists of elements that either satisfy all three cases, or see the lower-dimensional cases vanish at infinity. Choosing the boundaries of n-dimensional real spaces as n-1 spheres, the gauge field approaches a pure-gauge configuration with an action density that vanishes at infinity.

For finite actions, the group elements Ω may cover the entire group manifold of SU(2), which is a 3-sphere. The set of all classes in Hom(S3 → G) is the "third homotopy group of G". Families of maps associated with the group elements are pairwise non-intersecting, the minimal-action field configurations with asymptotic behavior of this type are stable, and solve the field equations.

For the static energy cases at infinity, those points at which ϕ₀ induces vanishing static energy density or static energy per line element. Either case is parametrized by 3- or 2-dimensional unit vectors. The stable field configurations lead to Hom(S2 → G/H) or Hom(S1 → G/H), neither of which is trivial. It implies that closed curves are not contractible on G/H. The associated topological stabilized field configurations of Hom(S2 → G/H) are finite-mass magnetic monopoles, where "charge" refers to the 3D charge described through the unbroken U(1) gauge group. It's topologically invariant and emerges from Hom(S2 → G/H) = ℤ. The fundamental group being nontrivial should be familiar at this point. Its topologically stabilized field configurations are infinitely long, magnetic vortex lines with a finite line density of mass. The 2D charge is topologically invariant.